Generative Market Theory
Zero-sum & Pareto-optimal frameworks imply tradeoffs: someone loses or must be left behind. Generative Market Theory (GMT) enables value creation without loss, exclusion, or sacrifice.
1. Definition
Definition 1 (Generative Market): A generative market is an economic system in which value V emerges endogenously through (i) multi-agent coordination, (ii) protocol-level design, and (iii) interaction with external entropy sources, such that value creation does not require redistribution, competitive exclusion, or Pareto tradeoffs.
Formally, a market M is generative if: There exists a change in value ΔV > 0 without any participant i experiencing a loss Li < 0.
Thus, net-positive outcomes may arise without any participant incurring harm or opportunity loss.
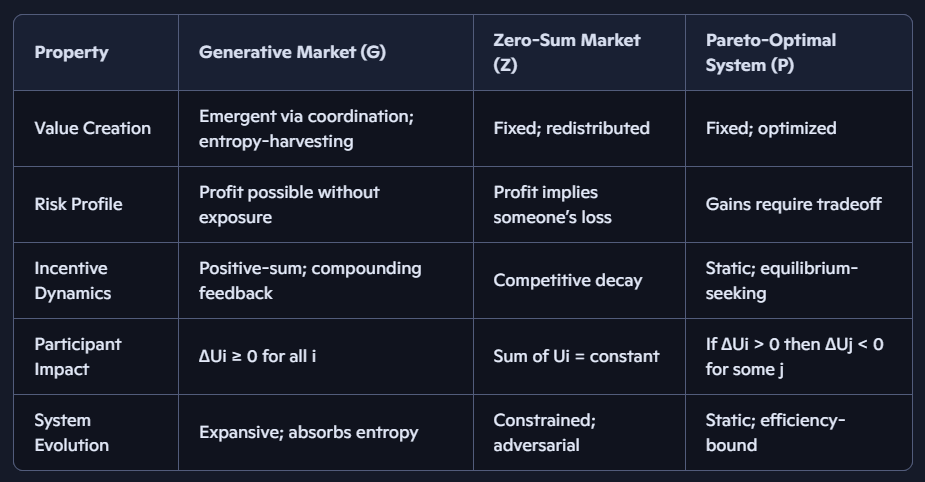
2. Core Properties
Let G denote a generative market, Z a zero-sum market, and P a Pareto-optimal system. Let Ui represent utility for participant i.
3. Kaspa as a Generative Substrate
Let K denote Kaspa’s BlockDAG protocol.
3.1 Throughput Abundance Proposition 1 (Non-Rivalrous Settlement Slots): Kaspa’s high-frequency block generation produces a superlinear supply of settlement opportunities. Let S(t) denote settlement capacity. In Kaspa, the partial derivative of S with respect to participant count is approximately zero, meaning additional activity does not reduce others’ access to blockspace.
3.2 Coordination Without Competition Proposition 2 (Non-Adversarial Extractive Processes): For arbitrageurs, miners, and users operating on K: ΔUi ≥ 0 for all i, because extraction of local inefficiencies does not diminish global resource availability.
3.3 Beyond Pareto Boundaries Proposition 3 (Adjacency Expansion): Let A(K) denote the set of feasible applications. Then the rate of change in the size of A(K) over time is greater than zero, without requiring removal, displacement, or reduction of existing applications—violating Pareto-bound assumptions of fixed-value frontiers.
3.4 ε-Episodes of Risk-Free Profit Kaspa permits temporary arbitrage intervals in which a participant can extract profit with bounded or zero exposure due to protocol-level ordering guarantees.
Definition 2 (Risk-Free Window): An ε-episode is an interval [t1, t2] where:
A price or structural inefficiency Vt exists with amplitude > ε
The hedged or atomic execution risk is < η, for η ≈ 0
These windows are especially amenable to oracle verification and automated exploitation.
4. Formal Claim of GMT
Claim (Generative Transformation): Kaspa instantiates a generative market G by satisfying:
Riskless Profitability: There exists ΔV > 0 with risk exposure ρ ≈ 0
Non-Harm Principle: ΔUi ≥ 0 for all i, ensuring no participant is harmed
Coordination-Based Value Creation: ΔV = f(protocol coordination, entropy), not from resource scarcity or competition
Thus, Kaspa transitions protocol design from an optimization framework to a generative one.
5. Falsifiability: Generative Episode Detection Loop
To empirically test GMT, define the measurable excursion set of detectable positive-sum inefficiencies.
Definition 3 (ε-Excursion Set): E(ε, δ) := {[a, b] | Vt > ε for all t in [a, b], and (b - a) ≥ δ}
Definition 4 (Generative Episode): A generative episode is a maximal connected interval [a, b] in E(ε, δ) such that:
Extractability: Profit Π > 0 is realizable
Non-Harm: ΔUi ≥ 0 for all participants
Coordination Source: ΔV arises from protocol-level interactions rather than rivalrous activity
This detection loop may be embedded in:
Trusted Execution Environments (TEEs)
Decentralized oracles
Smart contracts
to autonomously verify the presence or absence of generative behavior.
6. Conclusion
Generative Market Theory (GMT) describes a third category of market behavior beyond zero-sum and Pareto-optimized systems. Kaspa’s BlockDAG provides a concrete instantiation of this class by enabling:
Positive-sum value creation
Risk-free profitable episodes
Non-rivalrous coordination mechanisms
Thus, Kaspa functions as a generative substrate or an operational proof-of-concept that markets can create value without competition, tradeoffs, or redistribution.
Everyone wins and no one loses.
GMT is the first framework that describes a system where:
everyone can gain,
no one must lose,
no tradeoffs are required,
no redistribution is required,
and profit can emerge without risk.
Nothing in classical economics, game theory, mechanism design, or blockchain theory previously allowed this combination.
Kaspa creates infinite non-rivalrous settlement capacity, letting people build markets where no one competes for execution. As more people participate, the system makes more room so everyone wins simultaneously.